Koronakriisi on tuonut laskennallisilla malleilla tuotetun tiedon julkisen keskustelun aiheeksi. Vaikka mallintamiseen perustuva tieto on jo pitkään ollut keskeinen osa yhteiskunnallista päätöksentekoa, epidemiologisten mallien tuottamien ennusteiden, poliittisen päätöksenteon ja arjen yhteys on nykyisessä tilanteessa tuskallisen ilmeinen. Mallit näyttävät hallitsevan arkipäiväämme. Hieman kärjistäen, niiden tuottamat luvut määrittävät sen millä tahdilla yhteiskunnan toimintoja avataan. Samalla aikaa mm. THL:n tutkijat kuitenkin korostavat, että mallien ennusteet ovat epävarmoja, ja että “mallit eivät suoraan kerro, mitä todella tapahtuu tai mikä on totta”. (THL 11.5.2020,, s.18). Kaiken lisäksi eri mallit näyttävät tuottavan ratkaisevasti erilaisia ennusteita, jolloin käytetyn mallin valinnasta muodostuu tärkeä poliittinen päätös.
Ei siis ole mikään ihme, että tällaisen suurelta osin julkisuudelta piilossa olevan tietolähteen rooli demokraattisessa päätöksenteossa herättää kysymyksiä. Leo Lahti, Thomas Wallgren ja Markku Kulmala esittivät mielipidekirjoituksessaan (URL: https://www.hs.fi/mielipide/art-2000006494641.html), että THL:n käyttämien mallien lähdekoodi ja mallien parametrien arvioimiseen käytetyt aineistot tulisi avata julkisen kritiikin kohteeksi. Myös avoimen tiedon yhdistys Open Knowledge Finland esitti tietopyynnön mallien lähdekoodin avaamiseksi.
Voi siis näyttää siltä, että mallien käyttö politiikkaprosessissa tekee päätöksistä läpinäkymättömiä. Väitämme kuitenkin, että tilanne voi parhaassa tapauksessa olla täysin päinvastainen: verrattuna esimerkiksi asiantuntijalausuntoihin, mallien käyttö mahdollistaa tehokkaan monista tietolähteistä tulevan informaation integroimisen ja päätösten taustalla olevien päättelyiden näkyväksi tekemisen.
Verrattuna esimerkiksi asiantuntijalausuntoihin, mallien käyttö mahdollistaa tehokkaan monista tietolähteistä tulevan informaation integroimisen ja päätösten taustalla olevien päättelyiden näkyväksi tekemisen.
Mutta mitä mallit oikeastaan ovat ja minkälaista tietoa ne tuottavat? Muun muassa pienoismalleja, eläinmalleja, matemaattisia malleja ja tietokonesimulaatioita yhdistää se piirre, että malli toimii ikään kuin kohteensa edustajana. Mallijärjestelmää tutkimalla pyritään oppimaan jotakin kohteesta, joka itse saattaa olla esimerkiksi liian pieni (alkeishiukkanen), suuri (aurinkokunta) tai hankalasti kokeellisesti tutkittavissa (kansantalous). Tässä kirjoituksessa keskitymme laskennallisiin ja matemaattisiin malleihin.
Tutkijayhteisön ulkopuolelle mallit saattavat helposti näyttää tulevaisuutta ennustavilta kristallipalloilta, jolloin päätöksenteossakin tulisi kuunnella sitä tahoa, jolla on paras kristallipallo. Tieteellisten mallien ja mallinnettavan todellisuuden suhde on myös tiedeyhteisön sisällä kiistanalainen aihe. Yksityiskohtaisia tapaustutkimuksia tekevät sosiologit kummastelevat räikeitä yksinkertaistuksia käyttäviä taloustieteilijöitä, ja laboratorioissa kokeita suorittavat biologit epäilevät, mitä maailmasta oikeastaan voi oppia vain tietokonetta käyttämällä. Tieteenfilosofiassa onkin viime vuosina keskusteltu paljon tästä mallien ja maailman välisestä suhteesta sekä mallien käytöstä poliittisen päätöksenteon tukena.
Tieteellisten mallien ja mallinnettavan todellisuuden suhde on myös tiedeyhteisön sisällä kiistanalainen aihe.
Mitä mallit siis ovat? Oletetaan että tutkija on kerännyt havaintoaineiston, jossa ominaisuus y näyttäisi silmämääräisesti esiintyvän yhdessä kaksinkertaisen määrän ominaisuutta x kanssa. Koska tutkija ei luota silmämääräiseen mutuiluunsa, hän muotoilee matemaattisen kuvauksen tästä suhteesta (y = 2x), jota hän voi nyt verrata aineistoonsa ja näin arvioida alustavan hypoteesinsa luotettavuutta. Tutkija on näin luonut yksinkertaisen empiirisen (data) mallin. Tai kuvitellaan että tutkija kehittelee teoreettista hypoteesia, jonka seurauksena ominaisuudesta x seuraisi puolikas määrä ominaisuutta y. Koska tutkija ei taaskaan luota pelkkään järkeilyynsä ja mielikuvitukseensa, hän kirjoittaa tämän suhteen matemaattiseen muotoon, joka mahdollistaa hypoteesin loogisten seurauksien johtamisen luotettavalla ja tarkistettavissa olevalla tavalla. Tutkija on näin rakentanut teoreettisen mallin. Malliaan käyttämällä tutkija päättelee, että mikäli tietyssä populaatiossa suureen x arvo on 17468, voidaan päätellä että y:n arvo on vastaavasti 8734.
Todelliset tieteelliset mallit ovat tietenkin monin verroin monimutkaisempia, sisältäen enemmän muuttujia ja ratkaisevasti monimutkaisempia suhteita muuttujien välillä. Mallien muuttuessa monimutkaisemmiksi tulosten johtaminen analyyttisesti käy nopeasti mahdottomaksi ja tulosten laskeminen on annettava tietokoneen hoidettavaksi. Näin mallit muuttuvat käyttäjän näkökulmasta enemmän kokeiden kaltaisiksi: malleihin kohdistetaan virtuaalisia toimenpiteitä ja ne tuottavat ikään kuin uutta havaintoaineistoa, joka täytyy vuorostaan erikseen tulkita. Tämä ei kuitenkaan muuta mallien ja niistä johdettavan tiedon perusluonnetta miksikään: mallien tehtävä on avustaa päättelyä annetuista oletuksista johtopäätöksiin. Mallit eivät siis ole kokeita tai kristallipalloja, koska niillä ei ole mitään oletuksista riippumatonta suhdetta mallinnettavaan todellisuuteen.
Mallit eivät ole kokeita tai kristallipalloja, koska niillä ei ole mitään oletuksista riippumatonta suhdetta mallinnettavaan todellisuuteen.
Esimerkiksi paljon keskustelua herättänyt THL:n käyttämä malli on itse asiassa varsin yksinkertainen. Malli koostuu olennaisesti neljästä differenssiyhtälöstä, jotka kuvaavat kuinka alttiiden, tarttunnan saaneiden, tartuttavien ja immuunien osuudet koko väestöstä muuttuvat ajan mukana toisistaan riippuen (mallin nimi SEIR tulee mallin kuvaamasta neljästä vaiheesta: Susceptible – Exposed – Infectious – Removed). Huomisen osuudet määräytyvät tämänpäiväisten osuuksien mukaan. Mallissa väestö siis ikään kuin valuu alttiudesta tartuntojen kautta immuniteettiin. Yhtälöissä on kolme keskeistä parametria (perustartuttavuusluku sekä latentin vaiheen ja tartuttavuuden kestot), jotka säätelevät tämän valumisen nopeutta. THL:n SEIR ottaa lisäksi huomioon Suomen väestön ikärakenteen ja eri ikäryhmien välisten kontaktien määrät (jotka perustuvat aikaisempaan mittavaan empiiriseen tutkimukseen).
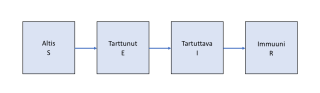
Nyttemmin THL on siirtynyt käyttämään nk. oppivia malleja, mutta niidenkin ytimessä on sama SEIR-malli. Mallin parametreja (esim. R0-luku, tartuntojen määrä, vuode/tehohoidon suhteellinen tarve) pyritään nyt arvioimaan erilaisia empiirisiä aineistoja käyttämällä (vuodehoitopotilainen määrä, tehohoitopotilaiden määrä, vasta-ainetestien tulokset). Mallin oppiva luonne tarkoittaa, että todellisia parametrien arvoja etsitään ajamalla mallia erilaisilla parametriarvojen yhdistelmillä samalla tarkastellen sitä, kuinka hyvin näin tuotetut ennusteet vastaavat empiirisiä aineistoja. Tällä tavoin saadaan muodostettua arviot havaintojen kanssa parhaiten yhteen sopivista parametrien arvoista sekä niihin sisältyvästä epävarmuudesta.
Eli vielä tiivistäen, mikäli malliin koodatut “teoreettiset” oletukset epidemian luonteesta ovat paikkansapitäviä ja eivät jätä huomiotta relevantteja piirteitä siihen liittyvistä prosesseita, malli kertoo millaisia parametrien arvoja meidän on rationaalista/järkevää pitää uskottavampina kuin toisia. Etenkin “oppivat” (Bayesilaiset) mallit tuottavat myös arvioita epävarmuuksista, joita näihin arvioihin sisältyy. Mutta se, että jokin malli (esim. THL:n oppiva SEIR-malli) antaa tietynlaisia ennusteita epidemian havaitsemattomista ominaisuuksista ei sulje pois mahdollisuutta, etteikö joku toinen malli, joka tekee erilaisia rakenteellisia oletuksia epidemiasta, voisi olla totuudenmukaisempi kuin nyt käytetty malli. Mallintaminen ei siis automaattisesti sulje pois muita mahdollisia teorioita tai selityksiä, vaan nuo mallien väliset vertailut pitäisi tehdä erikseen.
Vaikka THL:n käyttämä oppiva malli sisältää alkuperäiseen SEIR-malliin nähden huomattavasti enemmän liikkuvia osia, on olemassa myös sitä huomattavasti monimutkaisempia epidemiamalleja. Mallinnuksen kohteena voi esimerkiksi olla jokin tietty kaupunki, jolloin päämääränä on ottaa huomioon esimerkiksi työmatkaliikenteen reitit ja ajankohdat, pullonkaulat, julkinen liikenne ymv. (esim. EpiSims (Eubank et al. 2004) ja ruotsalainen MicroSim (Brouwers at al. 2009).
Vaikka tällaisten mallien käyttäminen saattaa vaikuttaa kokeenkaltaiselta toiminnalta (ja tällaisia monimutkaisia malleja käytetään usein erilaisten mahdollisten skenaarioiden tutkimiseen), on nytkin mallin tekemässä työssä kyse pohjimmiltaan numeeristen seurauksien johtamisesta erilaisista alkuoletuksista. Laskukone on vain monimutkaisempi.
Miksi mallinnusta tehdään?
Jos mallit eivät “suoraan kerro totuutta” (kuten THL:n materiaaleissa todetaan), miksi niille annetaan niin paljon painoarvoa? Mallit ovat olennaisesti päättelyn apuvälineitä. Esimerkiksi epidemian kulun ennustamiseksi meidän tulisi osata arvioida useita olennaisia parametreja, jotka eivät ole suoraan havaittavissa. Voimme esimerkiksi havaita sairaalahoidossa olevien määrän, mutta emme todennäköisyyttä päätyä sairaalahoitoon tartunnan jälkeen. Havaitsemme todennetut tartunnat, mutta emme perustartuttavuuslukua. Tilanteen tekee ongelmalliseksi se, että tällaiset päättelyt havaittavista suureista parametreihin riippuvat monella tapaa toisistaan; esimerkiksi arvio siitä, miten todetut tartunnat heijastavat (biologista) tartuttavuutta riippuvat myös arvioista populaation rakenteesta, kontakteista, testaamisesta yms. Tällaisten päättelyjen välisten riippuvuuksien seuraaminen on käytännössä mahdotonta ilman ulkoista apuvälinettä, joka pitää huolen siitä, että havainnot ja erilaiset oletukset pysyvät keskenään yhteensopivina. Mallintaminen on tästä syystä välttämätöntä erilaisia empiirisiä aineistoja yhdistettäessä.
Varsinaisten piste-ennusteiden tuottamisen sijaan mallien keskeisempi rooli onkin usein tiedollisen epävarmuuden esiintuominen ja arviointi, sekä tämän epävarmuuden seurausten täsmällinen päättely. Mallin rakentaminen pakottaa ennustajan tekemään selväksi kaikki ennusteeseen vaikuttavat oletukset sekä näiden oletusten keskinäiset riippuvuussuhteet – sekä itselleen että muille.
Mallinnuksella tuotetut ennusteet ovatkin näin monella tavoin läpinäkyvämpiä kuin asiantuntija-arviot: ennusteiden perusteet ovat, ainakin ideaalitapauksessa, kaikkien tarkistettavissa ja kritisoitavissa ja mallinnus toistettavissa. Asiantuntijalta voi toki kysyä, mihin hänen arvionsa perustuu, mutta asiantuntijan pään sisällä tapahtuva harkintaprosessi on kriittisen yleisön ulottumattomissa. Ennustemalleja ei muutenkaan käytetä kristallipallon tavoin (katsomalla mitä malli näyttää ja tyytymällä siihen). Monimutkaisten ennustemallien käyttö on pikemminkin vuoropuhelua mallin käyttäjien, mallin ja empiirisen aineiston kanssa. Tässä vuoropuhelussa synnytetty “tulos” kulkee lisäksi vielä usean tulkinnallisen vaiheen läpi ennen osallistumistaan päätöksentekoon.
Teoreettiset mallit pyrkivät kuvaamaan tarkasti vain jotakin tiettyä todellisuuden ilmiöön vaikuttavaa mekanismia, ja niitä ei tästä syystä ole pääsääntöisesti edes mielekästä pyrkiä sovittamaan sellaisenaan havaintoaineistoon.
SEIR-malli on hyvin empiirinen: se perustuu mahdollisimman suoraan mitattaviin trendeihin ja kohtalaisen suoraviivaisesti pääteltäviin parametriarvoihin. Se ei sellaisenaan pyri kuvaamaan esimerkiksi kaikkia tartuttavuuteen tai sairauden vakavuuteen vaikuttavia tekijöitä. Malli ei myöskään pidä sisällään pieniä ihmisiä, jotka reagoisivat muuttuviin olosuhteisiinsa (esimerkiksi MicroSim on tälläinen toimijapohjainen malli). Mallin tarkoitus on siis pääsääntöisesti kuvata ja ennustaa havaittavissa olevia ilmiöitä, ei niinkään selittää, mistä havaitut muutokset johtuvat. Täysin empiirinen (“fenomenologinen”) malli perustuu vain aineistossa esiintyviin säännönmukaisuuksiin. Fenomenologinen malli on usein paras väline puhtaisiin ennustetehtäviin, mutta siitä ei voi päätellä, mitä tapahtuisi jos mallinnettavaan ilmiöön kohdistettaisiin uudenlaisia toimenpiteitä. Tähän tarvitaan kausaalimalli, joka perustuu havaintojen lisäksi oletuksiin siitä, miten muuttujat vaikuttavat toisiinsa – ts. mitkä ovat syitä ja mitkä seurauksia. Teoreettiset mallit pyrkivät kuvaamaan tarkasti vain jotakin tiettyä todellisuuden ilmiöön vaikuttavaa mekanismia, ja niitä ei tästä syystä ole pääsääntöisesti edes mielekästä pyrkiä sovittamaan sellaisenaan havaintoaineistoon.
Oppiva SEIR ei ole puhtaasti fenomenologinen malli, vaan se sisältää useita (yleisesti hyväksyttyjä) rakenteellisia oletuksia vaikutussuhteiden suunnasta. Tämä on välttämätöntä, koska mallin on ennustettava mitä tapahtuisi esimerkiksi hoidettavien määrälle, jos tietyn ikäryhmän kontakteja vähennetään ohjeistuksella tai rajoituksella. Mallien tulkittavuutta ja avoimuutta kuitenkin parantaisi aineistosta suoraan johdettavissa olevien ja kausaalisten taustaoletusten selkeämpi erottelu.
Kausaalisten väitteiden erottaminen havaittavista säännönmukaisuuksista on tärkeää myös diagnostisten kriteerien ja selittävien tekijöiden erottamisen kannalta. Otetaan yksinkertainen esimerkki. Jos tartuntoja jäljitettäessä päätetään, että vasta yli 15 minuutin oleskelu korona-positiivisen henkilön kanssa samassa huoneessa antaa syyn testata henkilö taudin varalta, ei tämän luonteeltaan diagnostisen rajauksen pohjalta ole syytä olettaa, etteikö tauti voisi tarttua myös lyhyemmän altistuksen kautta (tai jäädä tarttumatta pidemmän kontaktin seurauksena). 15 minuutin altistuskynnys lienee luonteeltaan tilastollinen yleistys, kun taas tartunnan saamisen selittää pisaroiden tai virusta sisältävän aerosolin joutuminen hengitysteihin.
Vastuullisen mallintamisen periaatteet
Malleja kritisoidaan usein liiallisesta yksinkertaisuudesta. Mallin kuin mallin tapauksessa onkin yleensä helppo huudella takapenkiltä, miksi sitä tai tätä tärkeältä vaikuttavaa seikkaa ei ole sisällytetty malliin (esimerkiksi miksei nykyistä epidemiaa mallinneta verkostomalleilla, koska tartuttavuus ilmeisesti vaihtelee suuresti kantajasta toiseen. Jos näin on, yksi mahdollisesti tehokas tapa epidemian hallintaan olisi identifioida ja kohdistaa toimenpiteitä nimenomaan keskeisiin yksilöihin, joiden kyky tartuttaa muita on korkea). Laskennallisten mallien tapauksessa uusien tekijöiden lisääminen on lisäksi usein teknisesti varsin vaivatonta. On kuitenkin liuta hyviä perusteita sille, miksi niin teoreettiset kuin empiiriset mallit on tarpeen pitää mahdollisimman yksinkertaisina.
Ensinnäkin minkä tahansa uuden tekijän lisääminen tapahtuu aina jollain tietyllä täsmällisellä, mutta samalla väistämättä hieman mielivaltaisella, tavalla, ja tämä tuo lähes välttämättä mukanaan uusia epärealistisia oletuksia, joilla saattaa olla merkitystä mallin tuloksiin ja niiden tulkintaan. Tarkastellaan esimerkkinä mallissa tehtyä lineaarisuusoletusta: Vaikka lisätty tekijä itsessään olisikin todellisuudessa merkittävä, sillä että se on mallinnettu juuri lineaarisesti vaikuttavana tekijänä saattaa olla mallissa seurauksia, jotka eivät vastaa mitään ilmiötä mallinnettavassa todellisuudessa.
Monimutkaisten mallien tuloksia on myös vaikeampi tulkita, koska se, mistä oletuksista tulokset oikeastaan riippuvat, ei välttämättä ole selvää. Yksinkertainen muutaman muuttujan malli taas on käytettävyydeltään parempi päättelykone, koska muuttujien väliset riippuvuudet on helpompi kaivaa esiin.
Puhtaiden ennustemallien kohdalla liika monimutkaisuus kostautuu myös siksi, että mitä monimutkaisempi malli on, sitä todennäköisemmin se erehtyy luulemaan jotakin käytettävissä olevassa aineistossa esiintyvää satunnaisuutta todellista ennustuskykyä parantavaksi säännönmukaisuudeksi (tätä kutsutaan mallin ylisovittumiseksi). Monimutkaisten mallien notkeutta kuvaakin hyvin John Von Neumannin tokaisu, että neliparametrisen mallin kuvaajalla hän voi piirtää elefantin muodon, ja viidennellä parametrilla saa sen vielä heiluttamaan kärsäänsä.
Oli kyseessä sitten puhdas ennustemalli tai teoreettinen malli, malleihin väistämättä sisältyvät epätodet oletukset ja yksinkertaistukset johtavat ennusteiden epävarmuuteen ja virheellisten tulosten mahdollisuuteen. Tästä syystä mallien tuloksia tulisi aina koetella varioimalla systemaattisesti käytettyjä oletuksia. Käytettyyn aineistoon ja parametriarvoihin liittyvän epävarmuuden vaikutusta mallin tuottamiin tuloksiin voidaan usein helposti arvioida kvantitatiivisesti, mutta itse mallin rakenteesta johtuvien virheiden mahdollisuutta ei ole mahdollista arvioida yhtä täsmällisesti. Siksi ennusteiden tekemisessä olisikin hyvä käyttää myös useita kokonaan erilaisia mallialustoja (tällöin puhutaan ensemble-mallintamisesta).
Poliittisen vastuun siirtäminen tieteen tiedolliselle auktoriteetille on houkuttelevaa etenkin tilanteessa, jossa epävarmuudet ovat merkittäviä ja panokset suuria. Malli ei kuitenkaan lopulta voi olla vastuussa mistään. Tiedollinen vastuu on pääasiallisesti tutkimusprosessin jäsenillä kuten aineiston kerääjillä ja mallintajilla, kun vastuu päätöksistä taas on luonteeltaan poliittista vastuuta.
Tässä suhteessa THL:n käytäntö eroaa mielenkiintoisella tavalla Ruotsin FHM:n toiminnasta. Vaikka THL onkin kertonut tarkistaneensa tulostensa vakautta ajamalla mm. Imperial Collegen mallia suomalaisella aineistolla, nojaavat THL:n arviot selkeästi yhteen keskeiseen malliin. FHM sen sijaan ei käytä yhtä mallia aineiston yhdistämiseen ja ennustamiseen, vaan pikemminkin useita erillisiä kysymys-spesifisiä malleja asiantuntija-arvioiden tukena. FHM:n ennustestrategia on ilmeisesti kokonaisuudessaan vähemmän mallivetoinen kuin THL:n vastaava. FHM on myös salamyhkäisempi näiden laskennallisten apuvälineiden käytöstä kuin THL. Emme tässä ota kantaa siihen, kumman laitoksen ennustestrategia on viime kädessä järkevämpi. On kuitenkin syytä huomauttaa, että pääpiirteiltään avoimeen malliin ja aineistoon perustuva ennustaminen on läpinäkyvämpi toimintatapa kuin pelkkiin asiantuntija-arvioihin nojaaminen. Avoimen ennustemallin kristallipallo on ainakin periaatteessa avattavissa, testattavissa ja kritisoitavissa, kun taas asiantuntijakokouksista on parhaassakin tapauksessa saatavilla vain pöytäkirjat.
Näin siis periaatteessa.
Mutta vaikka etenkin tieteellisessä tutkimuksessa avoimen tieteen periaatteet ovat viime vuosina lisänneet mallintamisen avoimuutta, on läpinäkyvyyteen käytännön tasolla usein vielä matkaa. Läpinäkymätön mallien käyttö hämärtää helposti tiedollisen ja poliittisen vastuun paikantamista: huonosta päätöksestä on helppo syyttää huonoa mallia. Tämä huomio koskee kuitenkin kaikkea tieteellistä asiantuntijuutta. Kuten viime aikoina on nähty, poliittisen vastuun siirtäminen tieteen tiedolliselle auktoriteetille on houkuttelevaa etenkin tilanteessa, jossa epävarmuudet ovat merkittäviä ja panokset suuria. Malli ei kuitenkaan lopulta voi olla vastuussa mistään. Tiedollinen vastuu on pääasiallisesti tutkimusprosessin jäsenillä kuten aineiston kerääjillä ja mallintajilla, kun vastuu päätöksistä taas on luonteeltaan poliittista vastuuta.